Tag: Superposition

Exploring Quantum Computing and Wormholes: A New Frontier

 As we continue to unlock the secrets of quantum gravity and teleportation, each discovery invites us to ponder just how much more there is to unveil, a testament to the infinite possibilities that lie hidden within the quantum tapestry of our universe. The next revelation may be just around the corner, waiting to astonish us all over again, bringing us closer to understanding our universe, and our place within it.

Introduction

Imagine voyaging across the galaxy at warp speed, like in Star Trek or Star Wars, where starships zip through cosmic shortcuts called wormholes. While these cinematic adventures may seem far-fetched, the wildest twist is that wormholes aren’t just a figment of Hollywood’s imagination—quantum physics hints they might truly exist, emerging from the very fabric of quantum entanglement. This remarkable idea flips our understanding of the universe: space and time could actually spring from invisible quantum connections, reshaping what we know about black holes and the universe itself.

This revolutionary perspective burst onto the scene in 2013, thanks to Juan Maldacena and Leonard Susskind, who suggested that whenever two systems are maximally entangled, a wormhole connects them, anchoring each system at opposite ends [1]. Building on the pioneering work of Einstein, Podolsky, and Rosen (EPR) on quantum entanglement and the Einstein-Rosen (ER) description of wormholes, Maldacena and Susskind daringly bridged quantum physics with general relativity, inviting us to think of our universe as far stranger, and far more interconnected, than we ever imagined [2].

Einstein-Rosen Bridges and the Origins of Wormholes

In their seminal paper, Einstein and Rosen encountered the concept of wormholes while seeking to describe space-time and the subatomic particles suspended within it. Their investigation centred on disruptions in the fabric of space-time, originally revealed by German physicist Karl Schwarzschild in 1916, just months after Einstein published his theory of relativity.

Schwarzschild demonstrated that mass can become so strongly self-attractive due to gravity that it concentrates infinitely, causing a sharp curvature in space-time. At these points, the variables in Einstein’s equations escalate to infinity, leading the equations themselves to break down. Such regions of concentrated mass, known as singularities, are found throughout the universe and are concealed within the centres of black holes. This hidden nature means that singularities cannot be directly described or observed, underscoring the necessity for quantum theory to be applied to gravity.

Einstein and Rosen utilized Schwarzschild’s mathematical framework to incorporate particles into general relativity. To resolve the mathematical challenges posed by singularities, they extracted these singular points from Schwarzschild’s equations and introduced new variables. These variables replaced singularities with an extra-dimensional tube, which connects to another region of space-time. They posited that these “bridges,” or wormholes, could represent particles themselves.

Interestingly, while attempting to unite particles and wormholes, Einstein and Rosen did not account for a peculiar particle phenomenon they had identified months earlier with Podolsky in the EPR paper: quantum entanglement. Quantum entanglement led quantum gravity researchers to fixate on entanglement as a way to explain the space-time hologram.

Space-Time as a Hologram

The concept of space-time holography emerged in the 1980s, when black hole theorist John Wheeler proposed that space-time, along with everything contained within it, could arise from fundamental information. Building on this idea, Dutch physicist Gerard ‘t Hooft and others speculated that the emergence of space-time might be similar to the way a hologram projects a three-dimensional image from a two-dimensional surface. This notion was further developed in 1994 by Leonard Susskind in his influential paper “The World as a Hologram,” wherein he argued that the curved space-time described by general relativity is mathematically equivalent to a quantum system defined on the boundary of that space.

A major breakthrough came a few years later when Juan Maldacena demonstrated that anti-de Sitter (AdS) space—a theoretical universe with negative energy and a hyperbolic geometry—acts as a true hologram. In this framework, objects become infinitesimally small as they move toward the boundary, and the properties of space-time and gravity inside the AdS universe precisely correspond with those of a quantum system known as conformal field theory (CFT) defined on its boundary. This discovery established a profound connection between the geometry of space-time and the information encoded in quantum systems, suggesting that the universe itself may operate as a vast holographic projection.

ER = EPR

Recent advances in theoretical and experimental physics have leveraged the SYK (Sachdev-Ye-Kitaev) model to explore the practical realization of wormholes, particularly in relation to quantum entanglement and teleportation. Building on Maldacena’s 2013 insight that suggested a deep connection between quantum entanglement (EPR pairs) and wormhole bridges (ER bridges)—summarized by the equation ER = EPR—researchers have used the SYK model to make these ideas more tangible. The SYK model, which describes a system of randomly interacting particles, provides a mathematically tractable framework that mirrors the chaotic behaviour of black holes and the properties of quantum gravity.

In 2017, Daniel Jafferis, Ping Gao, and Aaron Wall extended the ER = EPR conjecture to the realm of traversable wormholes, using the SYK model to design scenarios where negative energy can keep a wormhole open long enough for information to pass through. They demonstrated that this gravitational picture of a traversable wormhole directly corresponds to the quantum teleportation protocol, in which quantum information is transferred between two entangled systems. The SYK model enabled researchers to simulate the complex dynamics of these wormholes, making the abstract concept of quantum gravity more accessible for experimental testing.

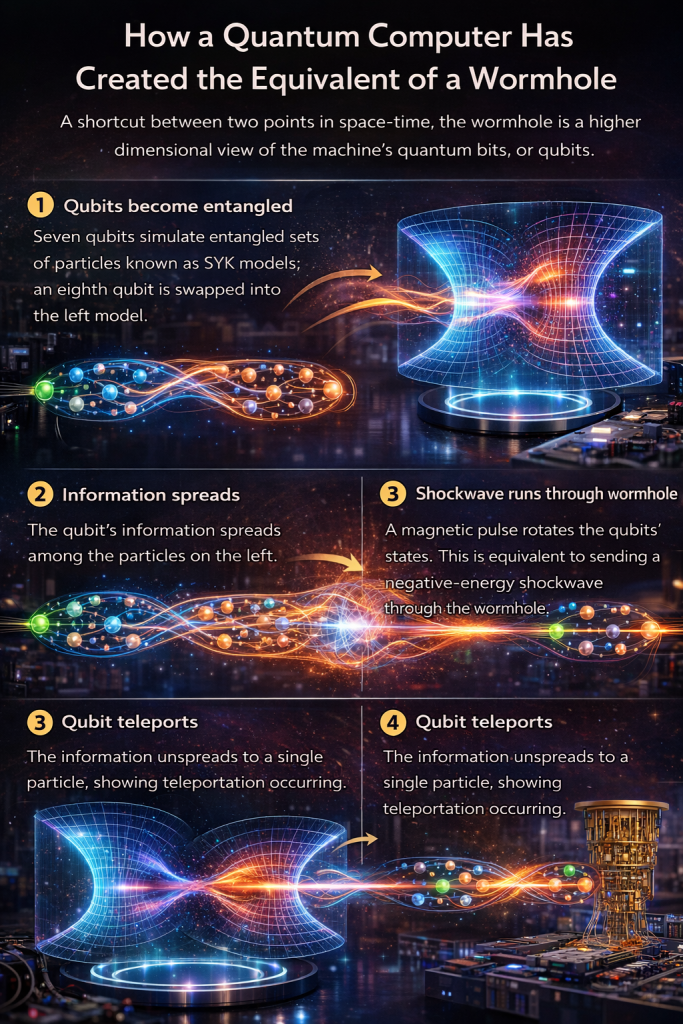
Fig 1. How a quantum computer simulated a wormhole

By 2019, Jafferis and Gao, in collaboration with others, successfully implemented wormhole teleportation using the SYK model as a blueprint for their experiments on Google’s Sycamore quantum processor. They encoded information in a qubit and observed its transfer from one quantum system to another, effectively simulating the passage of information through a traversable wormhole as predicted by the SYK-based framework. This experiment marked a significant step forward in the study of quantum gravity, as it provided the first laboratory evidence for the dynamics of traversable wormholes, all made possible by the powerful insights offered by the SYK model.

Conclusion

Much like the mind-bending scenarios depicted in Hollywood blockbusters such as Star Trek and Star Wars, where spaceships traverse wormholes and quantum teleportation moves characters across galaxies, the real universe now seems to be catching up with fiction.

The remarkable journey from abstract mathematical conjectures to tangible laboratory experiments has revealed a universe far stranger, and more interconnected, than we could have ever imagined. The idea that information can traverse cosmic distances through the fabric of space-time, guided by the ghostly threads of quantum entanglement and the mysterious passageways of wormholes, blurs the line between science fiction and reality.

 As we continue to unlock the secrets of quantum gravity and teleportation, each discovery invites us to ponder just how much more there is to unveil, a testament to the infinite possibilities that lie hidden within the quantum tapestry of our universe. The next revelation may be just around the corner, waiting to astonish us all over again, bringing us closer to understanding our universe, and our place within it.

by Tags: , , , , , , Leave a comment

Beyond Barriers: How Quantum Tunneling Powers Our Digital and Cosmic World

From memory devices to the heart of stars

Consider the operation of a flash memory card, such as an SSD or USB drive, which is capable of data retention even when powered off; the immense energy output from the sun and stars; or research indicating the occurrence of enzyme catalysis and DNA mutation [1]. These diverse applications are unified by the quantum mechanical phenomenon known as quantum tunneling.

Quantum tunneling refers to the capacity of particles to penetrate energy barriers despite lacking the requisite energy to surpass these obstacles according to classical mechanics. This effect arises from superposition, which imparts wave-like characteristics to quantum-scale particles and permits probabilistic presence across multiple locations. The transmission coefficient, which quantifies the likelihood of tunneling, is determined by the barrier’s height and width, in addition to the particle’s mass and energy [2].

Application of the time-independent Schrödinger equation allows the decomposition of the particle’s wave function into components situated within and outside the barrier. By ensuring continuity of the wave functions at the boundaries, the transmission coefficient can be derived. This theoretical framework has been effectively utilized in various fields, including the development of scanning tunneling microscopes and quantum dots.

Running your digital world

Modern electronics exist in a delicate balance with quantum tunneling. At the heart of today’s microprocessors are advanced transistors, which depend on the quantum ability of electrons to traverse ultra-thin insulating barriers. This tunneling enables transistors to switch on and off at remarkable speeds while using minimal energy, supporting the drive for faster, more energy-efficient devices. As technology advances and the insulating layers within transistors are made thinner to fit more components onto a single chip, the probability of electrons tunneling through these barriers inevitably increases. This leads to unwanted leakage currents, which can generate excess heat and disrupt circuit performance. Such leakage is a major challenge, setting hard physical boundaries on how much further Moore’s law—the trend of doubling transistor density— can be extended.

Yet, the same quantum effect that poses challenges in mainstream electronics is ingeniously exploited in specialized components. Tunnel diodes, for example, are engineered with extremely thin junctions that encourage electrons to quantum tunnel from one side to the other. This property allows tunnel diodes to switch at incredibly high speeds, making them invaluable for high-frequency circuits and telecommunications technologies where rapid response times are essential.

Quantum tunneling is also fundamental to how data is stored in non-volatile memory devices such as flash drives and solid-state drives (SSDs). In these devices, information is retained by manipulating electrons onto or off a “floating gate,” separated from the rest of the circuit by a thin oxide barrier. When writing or erasing data, electrons tunnel through this barrier, and once in place, they remain trapped, even if the device is disconnected from power. This is why your photos, documents, and other files remain safely stored on a USB stick or SSD long after you unplug them.

In summary, quantum tunneling is both a challenge and a tool in modern electronics. Engineers must constantly innovate to suppress unwanted tunneling in ever-smaller transistors, while simultaneously designing components that rely on controlled tunneling for speed, efficiency, and reliable data storage. This duality underscores how quantum mechanics is not merely an abstract scientific theory, but a practical force shaping the infrastructure of everyday digital life.

Powering stars, chips, and qubits

On a cosmic scale, quantum tunneling is fundamental to the process by which stars, including the Sun, emit light. It facilitates the fusion of protons within stellar cores by enabling them to overcome their mutual electrostatic repulsion, thus allowing nuclear fusion to occur at temperatures lower than those required in a strictly classical context. The existence of life on Earth relies on this mechanism, as it powers the energy output of stars that sustain our planet. Insights into tunneling continue to inform research efforts aimed at developing fusion reactors, where analogous physical principles must be managed under controlled conditions rather than governed by stellar gravity.

In superconducting circuits, which comprise materials capable of conducting electric current without resistance, pairs of electrons known as Cooper pairs tunnel through thin insulating barriers called Josephson junctions. When cooled to near absolute zero, these systems enable billions of paired electrons to behave collectively as a single quantum entity. This phenomenon has resulted in devices with exceptional sensitivity for measuring voltage and magnetic fields. Additionally, Josephson junctions play a central role in the architecture of superconducting qubits, where precision control of tunneling between quantum states enables reliable quantum logic operations.

The Nobel Prize in Physics 2025 was awarded to John Clarke, Michael H. Devoret, and John M. Martinis for their pioneering work in designing a macroscopic system utilizing a Josephson junction. The system was composed of two superconductors separated by an ultra-thin oxide layer, only a few nanometers thick. This layer permitted electron tunneling, and the observed discrete energy levels were in complete conformity with quantum mechanical predictions, a notable accomplishment from both experimental and theoretical standpoints [3].

A feature, a bug, and a design principle

Imagine a world where the chemical foundations of life and technology remain a mystery. Without quantum mechanics, our understanding of chemical bonds would be impossibly incomplete, the very medicines that save lives daily could never be designed, and the machines and electronics we rely on in our daily lives would not be possible.

Quantum tunneling stands as a striking testament that quantum phenomena are not mere scientific oddities; they are the bedrock of modern innovation. The same quantum effect that challenges engineers by causing troublesome current leaks in ever-smaller transistors is deliberately harnessed for breakthroughs: non-volatile memory, lightning-fast diodes, atomic-resolution microscopes, and the frontier of quantum computing all depend on it.

Every second, billions of electrons tunnel invisibly within the technology that surrounds you, their quantum behaviour silently orchestrating our digital universe. Far from being an abstract theory, quantum mechanics is the invisible engine driving your phone, your computer, your lasers, and LEDs—the essential infrastructure of twenty-first century life. Our entire technological existence pivots on the strange but real phenomena of the quantum world, challenging us to see science not as distant or esoteric, but as the very substance of our everyday reality.

by Tags: , , , , , , Leave a comment

Exploring the Implications of Quantum Collapse on Computing

The measurement problem isn’t just theoretical; it directly affects the development of effective quantum computing … Ultimately, reducing errors and increasing algorithm success in quantum computing relies on a solid grasp of what happens during measurement.

Introduction

In quantum mechanics, superposition refers to a unique and intriguing phenomenon where quantum particles can exist in several states simultaneously. Without observation, a quantum system remains in superposition and continues to evolve following Schrödinger’s equation. However, when we measure the system, it collapses into a single, definite state.

This concept challenges our everyday experience with classical objects, which always appear to have specific, identifiable states. Numerous experiments have confirmed that atoms can occupy two or more distinct energy levels at once [1]. If undisturbed, an atom stays in superposition until measurement causes its quantum state to break and settle into one outcome.

But what does it mean to measure or observe a quantum system? Why should a system capable of existing in countless simultaneous states reduce to just one when observed? These fundamental questions form the core of the “measurement problem” in quantum mechanics, a puzzle that has intrigued scientists for over a century since the field was first developed.

The measurement problem

The concept of “measurement,” as addressed by the wave function, has long raised critical questions regarding both the scientific and philosophical underpinnings of quantum mechanics, with significant implications for our comprehension of reality. Numerous interpretations exist to explain the measurement problem, which continues to challenge efforts to establish a coherent and reliable account of the nature of reality. Despite over a century of advancement in quantum mechanics, definitive consensus remains elusive concerning its most fundamental phenomena, including superposition and entanglement.

Quantum mechanics dictates that a quantum state evolves according to two distinct processes: if undisturbed, it follows Schrödinger’s equation; when subjected to measurement, the system yields a classical outcome, with probabilities determined by the Born rule. Measurement refers to any interaction extracting classical information from a quantum system probabilistically, without facilitating communication between remote systems [2]. This framework allows the measurement problem to be categorized into three principal issues:

  • Preferred basis problem – during measurement, outcomes consistently manifest within a particular set of states, although quantum states can, in theory, be described by infinitely many mathematical representations.
  • Non-observability of interference problem – observable interference effects arising from coherent superpositions are limited to microscopic scales.
  • Outcomes problem – measurements invariably produce a single, definitive result rather than a superposition of possibilities. The mechanism behind this selection and its implications for observing superposed outcomes remain unclear.

Addressing any one of these challenges does not fully resolve the others, thereby perpetuating the complexities inherent in the measurement problem.

Wave function collapse

The superposition of an atom across all possible states is characterized by a wave function, which serves as a representation of every quantum state and the probability associated with each state [3]. This function illustrates how an electron within an atomic cloud may occupy various positions with corresponding probabilities, and similarly how a qubit in a quantum computer can be in both states 0 and 1 simultaneously.

In the absence of observation, the system evolves continuously, maintaining the full spectrum of probabilities. Measurement, however, results in a distinct outcome; the act of measurement compels the selection of a single result from myriad possibilities, causing alternative outcomes to cease. As formalized by John von Neumann in 1932, quantum theory reliably predicts the statistical distribution of results over repeated trials, though it remains impossible to forecast the precise outcome of any individual measurement.

The wave function underscores the inherent randomness in the determination of outcomes, akin to nature employing chance. Albert Einstein famously critiqued this perspective, suggesting it implied that “God is playing dice” with the universe. Despite its counterintuitive nature, the wave function is essential for translating the stochasticity of superposition into the observed singular outcome, determined by the probabilities encoded within the wave function.

Conclusion

Wave function collapse plays a key role in quantum mechanics, linking the quantum and classical worlds. This phenomenon lets us measure things like an electron’s position and operate qubits in quantum computers, ensuring accurate results through coherence. Building dependable quantum computers largely depends on managing wave function collapse, aiming to prevent early collapses and errors while encouraging collapses that yield useful data.

The measurement problem isn’t just theoretical; it directly affects the development of effective quantum computing. Quantum algorithms work by sampling from a superposition of computational paths and collapsing them into desired outcomes, especially when designed well. Wave function collapse determines whether qubits are measured as intended or accidentally disrupted by outside influences (decoherence). Ultimately, reducing errors and increasing algorithm success in quantum computing relies on a solid grasp of what happens during measurement.

by Tags: , , , , , , 1 Comment

The Quantum Realm: Our Connection to the Universe

At the quantum scale, the universe manifests as a field of infinite possibilities, where the electrons within our atoms move in clouds of probability, always shifting. Consequently, we, as humans composed of countless atoms, are an inseparable part of the universe’s ever-changing nature, and our problems, at the quantum level, do not really exist.

Introduction 

When we close our eyes and place our hand on our forehead, we perceive the firmness of our hand and the gentle warmth of our skin. This physical sensation, the apparent solidity and presence of our body, seems tangible and reassuring. However, at the most fundamental level, our bodies are composed almost entirely of empty space. Beneath the surface of our bones, tissues, and cells, we find that our physical form is constructed from atoms, which themselves are predominantly made up of empty space, held together by the invisible forces of electromagnetism. The idea that we are, in essence, built from empty space can feel unsettling, yet it is central to our understanding of quantum mechanics.   

If we imagine an atom, and picture a single proton as a grain of sand placed at the centre of a football stadium, the nearest electron would be found somewhere in the outer bleachers, approximately 90 metres away. The vast expanse between the proton and the electron is filled with nothing but empty space [1]. The electrons themselves do not orbit the nucleus like tiny marbles following a fixed path. Instead, they ripple through space in a cloud-like manner, appearing in one location at one moment, and in another the next. Their movement is not governed by certainty, but by the probability clouds that define their position and momentum.    

The Universe Is Impermanent

Everything in the universe is in a state of constant motion. Objects such as chairs and tables may appear completely motionless to our eyes, yet at the quantum level, this sense of stillness is an illusion. Even as we sleep and perceive ourselves to be at rest, the atoms that make up our bodies are ceaselessly moving and vibrating. This underlying activity is dictated by the principles of quantum mechanics, which reveal an intricate and dynamic world beneath the surface of everyday experience.

Werner Heisenberg’s uncertainty principle states that it is impossible to simultaneously know both the precise position and the exact momentum of any object [2]. The more accurately we measure one, the less certain we become of the other. This fundamental limit means that no object can ever be fixed in a single, definite spot while remaining absolutely still. To do so would violate the laws of quantum physics, which require all matter to retain a degree of movement and uncertainty 

Consider a ball placed in a bowl and cooled until it appears perfectly still at the bottom. According to the uncertainty principle, the ball can never truly be at rest. It will always exhibit a subtle vibration, as restricting its position too precisely leads to uncertainty in its momentum. This perpetual motion is known as the ball’s zero-point energy.  

A universe where everything is perfectly still would not permit life as we know it. Nothing in the cosmos is permanent; particles continuously move, shift, and even appear and disappear. Remarkably, quantum theory predicts that even the vacuum of space is not empty but is filled with modes of vibration possessing zero-point energy [3]. This means that space itself is permeated by an endless and restless sea of energy, where particles are constantly popping in and out of existence, reflecting the ever-changing nature of reality.  

Quantum Mechanics and the Foundations of Consciousness 

At the quantum level, the behaviour of particles is defined by several extraordinary phenomena, including superposition, entanglement, coherence, and the observer effect. In the phenomenon known as superposition, particles can exist in multiple states at the same time. These particles remain in superposition until an act of observation occurs, causing their wave functions to collapse into a single, definite outcome. When two particles interact and become entangled, their properties, such as spin, polarization, and momentum, become fundamentally inseparable. Measurement of one entangled particle instantly determines the state of its partner, regardless of the distance separating them. 

Humans are deeply entangled with the inner workings of the universe. Our thoughts, memories, and emotions are rooted in the quantum behaviours of the atoms that compose our bodies. Consciousness, in this context, is shaped and defined through quantum operations. The billions of neurons firing simultaneously in the human brain function through quantum entanglement, collectively giving rise to our conscious experience [4]. 

Stuart Hameroff and Roger Penrose, in their 1996 paper, argued that consciousness depends on coherent quantum processes within collections of microtubules found in brain neurons. At the lowest neurophysiological level, the cytoskeleton of neurons in the human brain is composed of protein networks, specifically neurofilaments and microtubuli. These structures are essential for various transport processes within neurons [5] [6]. According to Hameroff and Penrose’s theoretical framework, tubulins in microtubuli serve as the substrate for quantum processes. 

Through their Orchestrated Objective Reduction (Orch OR) theory, Hameroff and Penrose proposed that the brain’s microtubules act as quantum computers, maintaining coherent quantum states that collapse in a process tied to the geometry of space-time and influenced by quantum gravity. In this framework, consciousness operates as a quantum wave function passing through the brain’s microtubuli, with these collapses corresponding to the observer’s elementary acts of consciousness and embedding them directly into the fabric of the universe. 

Conclusion 

Contemplating the foundations of our bodies and consciousness, it becomes apparent that quantum mechanics may govern much more than just the biological processes within us. While the Orch OR theory proposed by Hameroff and Penrose remains a topic of debate, it opens the door to the possibility that consciousness arises not solely from biological functions but also from quantum phenomena.

In quantum computing, the act of observation is inherently influential, determining the state to which a particle’s wave function collapses. This raises a profound question: could quantum mechanics provide an explanation for our ability to perceive and realize different realities within our consciousness? Furthermore, could our observation of quantum states, which shape our consciousness, be the very mechanism that connects us to the universe in a holistic manner?

I found that for me, the most meaningful way to think about it was that the concept of uncertainty and constant motion is central to how the universe operates at the quantum level. If our bodies and consciousness are subject to the laws of quantum physics, then our experiences of periods of darkness and despair, feelings of being stuck or hopeless, are never truly fixed states. Motion persists within our atoms and within our consciousness, regardless of our perceptions. The pressure we experience, the everyday stresses, and our emotions are all shaped by how we observe and interpret events. At the quantum level, nothing remains permanent; everything is in flux.

This perspective is not meant to diminish our existence as human beings. Rather, it highlights our intrinsic connection to the fabric of the universe. The universe does not operate with absolute certainty or permanence; it is defined by uncertainty, continual change, and movement. At the quantum scale, the universe manifests as a field of infinite possibilities, where the electrons within our atoms move in clouds of probability, always shifting. Consequently, we, as humans composed of countless atoms, are an inseparable part of the universe’s ever-changing nature, and our problems, at the quantum level, do not really exist.

Designing solutions that effectively meet user needs is the driving force behind my work. I also share practical insights on computing and human-centered design each week. I’d love to connect and discuss your design ideas or challenges; feel free to reach out to me today on LinkedIn or contact me at Mimico Design House.

by Tags: , , , , , , , , , , , , , 1 Comment

Quantum Computing: Revolutionizing Industry and Science

We can imagine a world where quantum computers will be able to design powerful new drugs by simulating the behaviour of individual molecules, and optimize complex supply chains to help companies source the parts they need and assemble products in the most efficient way possible.

Introduction

Quantum computing is an entirely new dimension of computing leveraging the laws of quantum mechanics. Quantum computers apply superposition and entanglement at the universe’s smallest scales and coldest temperatures. They also adopt a multidisciplinary approach comprising of computer science, physics and mathematics to enable scientist to solve complex problems.

While today’s quantum computers remain rudimentary and error-prone, they have the potential to provide significant performance gains, and dramatically increased computation speeds to perform complex computational tasks that can take classical computers years to complete. Numerous governments, universities and vendors around the world are investing heavily in harnessing quantum computing technology to achieve fault-tolerant and reliable systems.

In this article, I provide a detailed examination of the key concepts underlying quantum computers, and how they promise to open the potential for massive advancements in a variety of scientific and industrial applications.

Superposition and entanglement

Qubits are the most basic units of processing in quantum computers. Qubits rely on the use of particles such electrons and photons, that can be suspended in states of 0, 1 or any states in between. This ability of qubits to be in more than one state at a time is what gives quantum computers their processing power. However, it is the application of superposition and entanglement through interference to qubits that allow quantum computers to produce reliable outcomes.

To better understand superposition, we refer to the famous thought experiment involving a cat as imagined by the physicist, Erwin Shrödinger. Shrödinger’s experiment imagined a cat sealed in a box with a poison trap that can be triggered by a decaying radioactive atom. Since the decay of the radioactive atom is uncertain, at any given moment the cat could be in a superposition of states such that it is either dead or alive [1]. It is only when someone opens the box and observes the cat does its state become definite or its state “collapses” to being either dead or alive.

Superposition is difficult to explain through analogies; however it is also possible to imagine a coin tossed and spinning fast in the air. As long as the coin continues spinning then its state can be considered both heads and tails. It is only when the coin is stopped does one observe its state as either heads or tails.  

Quantum theory also implies that particles can be linked with each other, such that when the state of one particle changes it will instantly impact the state of the other, regardless of the distance between them. This is what is referred to as entanglement, and it is what allows qubits to correlate their states with each other and thus scale their processing power exponentially.

In Shrödinger’s cat experiment, entanglement can be described as having several cats in the box that are entangled in a superposition of states such all cats in the box are either dead or alive. When someone opens the box, their state then collapses such that the cats in the box are all observed to be either dead or alive. Entanglement means that two particles are always connected, and they are never independent of each other. This is how nature works at the atomic level.   

Interference

Quantum interference refers to a phenomenon where the probability amplitudes of quantum states combine, either constructively or destructively, to influence the likelihood of an outcome. In classical interference, physical waves such as sound or water can overlap such that they amplify or cancel each other out. Quantum interference is different in that is it based on the wave-like behaviour of particles such as electrons, photons and atoms [2].

In quantum theory, particles are described via wavefunctions, which contain complex-value probability amplitudes. We can think of a particle going through two indistinguishable paths such as two slits in a barrier as the two-slit experiment describes. In this experiment, particles such as photons or electrons are fired one at a time at a wall with two narrow slits and a screen placed behind it. Each particle must pass through slit A, slit B or a combination of both. The expectation would be that particles would pass through one slit or the other, and that the screen would show two bright spots as the particles pass through.

Instead of observing two spots on the screen, a series of bright and dark fringes are observed – an interference pattern. The fringe pattern is characteristic of the behaviour of waves rather than particles, where the bright areas indicate wave amplitudes that amplified each other, while the dark ones are waves that canceled out. This behaviour can be described as [3]:

  • Constructive interference, where the wave amplitudes add up, thus increasing the probability of a particular outcome.
  • Destructive interference, where the amplitudes cancel each other out, thus reducing or eliminating the chance of an outcome.

What is fascinating about the fringe pattern observed is that it can appear even when particles are sent one at a time. Therefore, instead of interfering with each other particles are interfering with themselves, thus taking both paths simultaneously in superposition.

Interference is what gives quantum computers their superiority over classical computers. It allows quantum systems to guide computations by enhancing the probability of correct answers while supressing wrong ones. Once qubits are transformed and entangled, their probability amplitudes evolve through interference. All possible computations are performed simultaneously and are allowed to interact through entanglement.

A critical condition of interference is that the paths followed by qubits are indistinguishable, such that it is not possible to determine which path a qubit takes, even in principle. Any form of measurement collapses the wavefunction, thus destroying the superposition and possibility of interference. Interference underlies the power of quantum computing, and it remains a key component in unlocking the full potential of quantum technology.

Measurement

In the final stage of quantum computing, states collapse into classical outcomes upon measurement. These outcomes are not random and are fundamentally determined by whether computational paths leading to them have interfered constructively or destructively.

A state where computational paths leading to it have interfered destructively will have a probability close to 0. Similarly, a state where computational paths leading to it have interfered constructively will have a significantly amplified likelihood.

Instead of measuring outcomes sequentially, quantum computers exploit the wave-like nature of qubits to allow all possible computational paths to co-exist and interfere. This creates a probabilistic landscape where the correct answers become the most likely outcomes.

Quantum bits (Qubits)

Computers process information using bits that store information using 0’s and 1’s. Bits can be represented using physical objects such as bar magnets or switches placed in either a state of up or down. Bits can maintain their state for a long time, thus allowing them to represent stored information in a stable and long-lasting fashion. However, bits are limited in their ability to store information when compared to qubits. While bits can exist in either a stare of 0 or 1, qubits can exist in a superposition of multiple states of 0, 1 or any state in between.

The superposition of qubits is what makes them superior to classical bits. It is possible to think of a qubit as an electron spinning in a magnetic field. The electron could be spinning with the field, known as spin-up state, or against the field, knows as spin-down state. Suppose it is possible to change the direction of the electron’s spin using a pulse of energy such as a laser. If only half a pulse of laser energy is used and all external influences are isolated, then we can imagine the electron in superposition where it is in all possible states at once [4].

Superposition increases the computational power of qubits exponentially depending on the number of qubits in a quantum computer. Whereas two classical bits can contain only two pieces of information (01 and 10), two qubits can store a superposition of four combinations of 0 and 1 simultaneously, three qubits can store eight combinations, and so on. Therefore, a quantum computer can perform 2N computations, where N is the number of qubits.

Conclusion

Through exponential scaling, unique algorithms and the continued evolution of quantum hardware, quantum computing has the potential to revolutionize industries like cryptography, material science, pharmaceuticals and logistics. We can imagine a world where quantum computers will be able to design powerful new drugs by simulating the behaviour of individual molecules, and optimize complex supply chains to help companies source the parts they need and assemble products in the most efficient way possible. Other more impactful applications could be computers that could break the encryption that safeguards our private information on the internet.

Governments, companies and research labs are working tirelessly to harness the potential of this emerging technology. Quantum computing, combined with the capabilities and advancements in AI, has the potential to achieve artificial general intelligence (AGI). By enabling rapid data processing and computation, improved learning capabilities and parallel processing, quantum computers can process extensive datasets, enabling the improved learning capabilities needed for AGI. As quantum computers continue to rapidly evolve, it is essential for us to harness their potential in ways that further advance humanity’s future and well-being.

References

[1] Quantum Computing Explained

[2] What is quantum interference and how does it work?

[3] Quantum interference in Quantum Computing: 2025 Full Guide

[4] What is quantum computing? How it works and examples

by Tags: , , , , , , , , , , , , , , , 1 Comment