Tag: Quantum Mechanics

Exploring Quantum User Experience: Future of Human-Computer Interaction

Introduction

In today’s rapidly evolving digital world, our interactions with technology are no longer limited to simple interfaces and straightforward feedback. The growth of cloud infrastructure, the explosion of big data, and the integration of advanced Artificial Intelligence (AI) have transformed the very foundation of how humans connect with systems. As applications become more intelligent, pervasive, and context-aware—operating seamlessly across devices in real-time—users expect more fluid, responsive, and personalized experiences than ever before. These expectations challenge the boundaries of traditional Human-Computer Interaction (HCI) and User Experience (UX) models, which were not designed for such complexity or dynamism.

Legacy frameworks like Human-Centred Design (HCD), User-Centred Design (UCD), the Double Diamond model, and Design Thinking have provided structure for decades, yet their sequential stages and lengthy feedback loops can’t keep pace with the demands of today’s interconnected, AI-driven world. To design experiences that truly resonate, we must rethink our approach—moving beyond rigid methodologies and embracing new paradigms that account for the unpredictable, adaptive nature of modern technology. The future of HCI calls for innovative, human-centred AI design strategies that acknowledge the unique capabilities and limitations of intelligent systems from the very start [1].

Quantum User Experience (QUX): An Alternative Perspective for HCI

When examining ways to enhance Human-Computer Interaction (HCI) methodologies, it becomes apparent that these approaches share similarities with the fundamental phenomena underlying nature and life itself. Drawing inspiration from Quantum Mechanics, we can establish a theoretical analogy to HCI, which gives rise to the concept of Quantum User Experience (QUX). QUX offers a distinct departure from traditional User Experience (UX) models in several ways [2]:

  • Fluidity: QUX is not rigid, thus enabling experiences to be more dynamic and adaptable.
  • Adaptability: QUX is not linear, allowing experiences to evolve in response to users’ changing needs.
  • Mathematical Foundation: QUX is not random; it leverages mathematical data derived from measurements and research on user behaviour. This approach integrates feedback from previous processes and their associated data into new experiences.
  • Temporal Definition: QUX is not infinite; experiences are distinctly defined in time, avoiding endless cycles of testing and iteration.

To reinforce this theoretical framework, the digital cosmos is conceptualized as the global network—such as the internet—functioning on two key scales: the macroscopic scale, which encompasses phenomena that are detectable, analyzable, and able to be influenced at a broad level across the network; and the microscopic scale, which refers to aspects that are perceived and felt, yet not directly observed or measured.

In the digital cosmos, three core entities serve as the foundation for its structure: Agents, Interactions, and Objects. Agents encompass not only users, but also any entity capable of engaging with others, such as bots, engines, or platforms. Interactions refer to the exchanges or communications that occur between these agents, facilitating connections and the flow of information. Objects represent the wide range of content found within the global network, including text, audio, and visual elements, all of which contribute to the richness and diversity of the digital environment.

Within the Quantum User Experience (QUX) framework, experiences are categorized as either macro- or micro-experiences: macro-experiences encompass collective behavioural patterns that involve multiple entities and significantly influence individuals or groups, while micro-experiences represent individual responses to notable stimuli or events that hold personal significance and shape one’s overall perception or feelings. Together, these experiences form the cumulative fabric of QUX, contributing to the flow of information across the vast structure of the digital cosmos.

Quantum-Scale Behaviour of Agents, Interactions, and Objects in QUX

Within the QUX framework, the behaviours of Agents, Interactions, and Objects can be interpreted through a quantum lens, revealing how microscopic traits and probabilistic states shape the digital cosmos.

Agents are entities that exhibit microscopic characteristics—such as cognitive, social, or psychological attributes—which manifest as observable macroscopic behaviours. In the QUX perspective, Agents are conceptualized as “strings,” drawing a parallel to String Theory. This analogy suggests that all observable phenomena within the digital cosmos, at a macroscopic level, originate from the various vibrational states of these strings.

Interactions encompass the diverse behaviours that occur between agents (as vibrating strings) and objects, influenced by users’ perceptions and experiences over time. These interactions function as probabilistic quantum systems in superposition, described by their intensity (the strength of the interaction) and frequency (the variance of the interaction over time). Upon measurement, these probabilistic states collapse into observable Quantum Experience (QXE) states, allowing for a flexible and probabilistic approach to modelling user engagement.

Objects are defined as probabilistic Experience Elements (XL), which serve as the fundamental building blocks—such as buttons—of a system, application, or service. These objects possess a spectrum of possible values governed by probabilities and are characterized by discrete Experience Quanta (XQ) energy units resulting from user interactions. This framework supports real-time adaptability and multivariate evaluation of experiences, surpassing the limitations of traditional, rigid A/B testing methods.

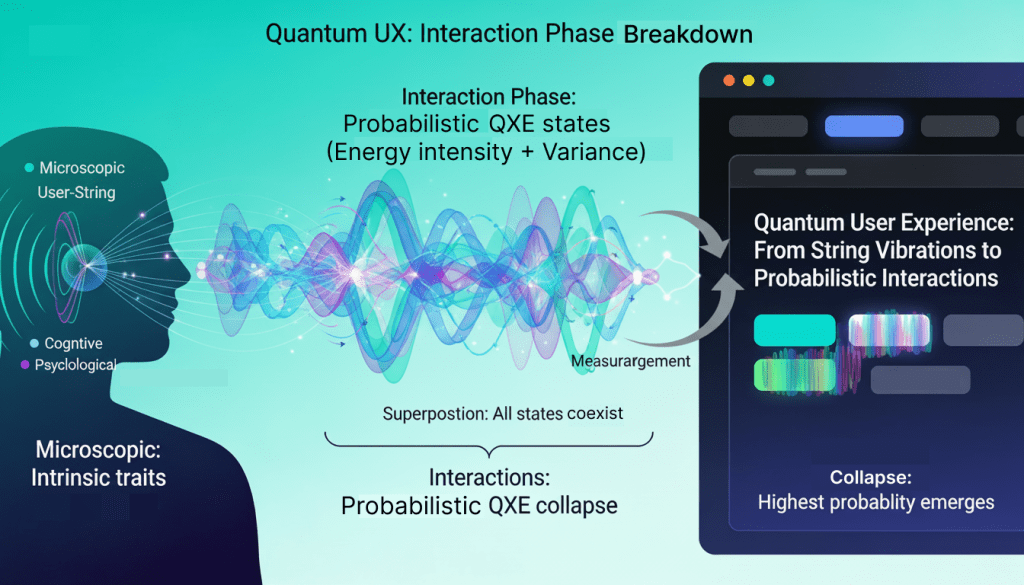
Fig 1. QUX phase breakdown. Micro experiences combine together to form a superposition of states, collapsing into highest probability quantum user experiences.

Conclusion: Quantum Mechanics as Inspiration for QUX

The QUX framework draws profound inspiration from quantum mechanics, reshaping our understanding of human-computer interaction by adopting concepts like superposition, probabilistic states, and collapse. By viewing agents as vibrating strings—much like those in String Theory—QUX reimagines the digital cosmos as a domain where microscopic traits and behaviours coalesce into observable, macroscopic phenomena. Interactions function as quantum systems, existing in probabilistic superpositions until measured, at which point they collapse into tangible Quantum Experience (QXE) states. Objects, conceptualized as probabilistic Experience Elements, embody the quantum notion of possible values and energy units that adapt in real-time to user input. This quantum-inspired perspective enables flexible modelling of engagement, surpassing the limitations of classical, deterministic approaches.

As cloud computing, artificial intelligence, and quantum technologies advance, QUX motivates a paradigm shift in human-centred design and methodology. It champions adaptability, multivariate evaluation, and responsiveness to evolving user needs—mirroring the uncertainty and dynamism at the heart of quantum mechanics. In this way, QUX not only offers a novel theoretical foundation, but also empowers designers to meet the demands of a rapidly evolving technological landscape, ensuring that applications and systems remain attuned to the nuanced and changing nature of user experience.

by Tags: , Leave a comment

Rethinking Reality: The Unwritten Story of Time

The universe is not a closed book, but rather a narrative in progress—its future pages unwritten, its history ever-expanding. The digits that define time, instead of being predetermined, seem to emerge in concert with our unfolding experience, hinting at a reality that is both participatory and creative.

Introduction

Time: we all experience its steady march, feel its passing in our bodies, and witness its effects as trees stretch skyward, animals age, and objects wear down. Our everyday understanding of time is one of motion—a ceaseless flow from past, to present, into an open future. Yet, what if the very nature of time is not what it seems? Physics offers a perspective that is at odds with our intuition, challenging us to rethink everything we believe about reality.

Albert Einstein’s revolutionary theory of relativity upended this familiar notion, proposing that time is not merely a backdrop to events, but a fourth dimension intricately woven into the fabric of the universe. In his “block universe” concept, the past, present, and future exist together in a four-dimensional space-time continuum, and every moment—from the birth of the cosmos to its distant future—is already etched into reality. In this cosmic tapestry, the initial conditions of the universe determine all that follows, leaving little room for the unfolding uncertainty we sense in our lives [1].

Contrasting Views: Einstein, Quantum Mechanics, and the Nature of Time

Most physicists today accept Einstein’s pre-determined view of reality, in which all events—past, present, and future—are fixed within the space-time continuum. However, some physicists who explore the concept of time more deeply find themselves troubled by the implications of this theory, particularly when the quantum mechanical perspective is considered. At the quantum scale, particles act in a probabilistic manner, existing in multiple states at once until measured; it is only through measurement that a particle assumes a single, definite state.

While each measurement of a particle is random and unpredictable, the overall results tend to conform to predictable statistical patterns. The behaviour of quantum particles is described by the evolution of their wave function over time. Quantum wave functions require a fixed spacetime, whereas relativity treats spacetime as dynamic and observer-dependent. This fundamental difference complicates efforts to develop a theory of quantum gravity capable of quantizing spacetime—a major challenge in modern physics [2].

Relativity, in contrast, insists that time and space be treated equally, making it necessary to introduce time as an operator and place it on the same level as position coordinates. In quantum mechanics, each particle is part of a system with many particles, and time and space coordinates are not treated equally. In such systems, there are as many position variables as there are particles, but only a single time variable, which represents a flaw in the theory. To overcome this, scientists have developed the many-time formalism, where a system of N particles is described by N distinct time and space variables, ensuring equal treatment of space and time [3].

If physicists are to solve the mystery of time, they must weigh not only Einstein’s space-time continuum, but the fact that the universe if fundamentally quantum, governed by probability and uncertainty. Quantum theory treats time in a very different way than Einstein’s theory. Time in quantum mechanics is rigid, not intertwined with the dimensions of space as it is in relativity.

Gisin’s Intuitionist Approach and Indeterminacy

Swiss physicist Nicolas Gisin has published papers aiming to clarify the uncertainty surrounding time in physics. Gisin argues that time—both generally and as we experience it in the present—can be expressed in intuitionist mathematics, a century-old framework that rejects numbers with infinitely many digits.

Using intuitionist mathematics to describe the evolution of physical systems reveals that time progresses only in one direction, resulting in the creation of new information. This stands in stark contrast to the deterministic approach implied by Einstein’s equations and the unpredictability inherent in quantum mechanics. If numbers are finite and limited in precision, then nature itself is imprecise and inherently unpredictable.

Gisin’s approach can be likened to weather forecasting: precise predictions are impossible because the initial conditions of every atom on Earth cannot be known with infinite accuracy. In intuitionist mathematics, the digits specifying the weather’s state and future evolution are revealed in real time as the future unfolds. Thus, reality is indeterministic and the future remains open, with time not simply unfolding as a sequence of predetermined events. Instead, the digits that define time are continuously created as time passes—a process of creative unfolding.

Gisin’s ideas attempt to establish a common indeterministic language for both classical and quantum physics. Quantum mechanics establishes that information can be shuffled or moved around, but never destroyed. However, if digits defining the state of the universe grow with time as Gisin proposes, then new information is also being created. Thus, according to Gisin information is not preserved in the universe since new information is being created by the mere process of measurement.

The Evolving Nature of Time

As we survey the landscape of contemporary physics, it becomes apparent that our classical conception of time is far from settled. Instead, it stands at the crossroads of discovery—a concept perpetually reshaped by new theories and deeper reflection. Einstein’s vision of a pre-determined reality, where all moments are frozen within the space-time continuum, offers comfort in its order and predictability. Yet, this view is challenged by the quantum world, where uncertainty reigns, and events transpire in a haze of probability until measurement brings them into sharp relief.

The friction between the determinism of relativity and the indeterminacy of quantum mechanics compels us to look beyond conventional frameworks. Quantum mechanics treats time as an inflexible backdrop, severed from the intricacies of space, whereas relativity insists on weaving time and space together, equal and dynamic. Gisin’s intuitionist approach further invites us to reflect on the very bedrock of reality—questioning whether information is static or endlessly generated as the universe unfolds.

This ongoing dialogue between classical physics and emerging quantum perspectives not only exposes the limitations of our current understanding but also sparks a profound sense of curiosity. If, as Gisin suggests, information is continuously created, then the universe is not a closed book, but rather a narrative in progress—its future pages unwritten, its history ever-expanding. The digits that define time, instead of being predetermined, seem to emerge in concert with our unfolding experience, hinting at a reality that is both participatory and creative.

by Tags: , , , , , Leave a comment

Quantum Revolution: How Max Planck Tapped Into the Universe’s Zero-Point Mysteries

Unveiling the Ever-Vibrant Fabric of Reality

Introduction

At the dawn of the twentieth century, Max Planck embarked on a quest to unravel how energy is absorbed and emitted by the filaments within light bulbs, aiming to maximize their efficiency and illuminate more while consuming less power. In doing so, Planck not only resolved practical engineering challenges, but also ignited a scientific revolution that fundamentally reshaped our comprehension of physics and the universe itself.

Planck’s investigations shattered the classical notion that energy flows in a seamless, continuous stream. Instead, he revealed that energy is exchanged in tiny, indivisible packets known as quanta. This radical insight gave birth to quantum theory, a new framework that challenged long-held assumptions and transformed our understanding of the physical world, from the behaviour of the smallest particles to the structure of the cosmos.

The significance of Planck’s discovery extends far beyond theoretical physics. By demonstrating that energy exchanges are quantized, he opened the door to a wave of scientific breakthroughs, paving the way for technologies such as semiconductors, lasers, and quantum computing. Moreover, subsequent research based on Planck’s work uncovered the existence of zero-point energy: even in the coldest conceivable state, where classical theory predicted absolute stillness, quantum systems retain a subtle but unceasing vibrancy. This revelation overturned the classical thermodynamic belief that all motion ceases at absolute zero, unveiling a universe in perpetual motion at its most fundamental level.

Planck’s legacy is profound, not only did he lay the foundations for quantum mechanics, but his insights continue to inspire new discoveries that help us probe the mysteries of existence. By deepening our grasp of reality’s underlying fabric, Planck’s work has transformed how we see our place in the universe, inviting us to explore how the strange and wonderful quantum world shapes everything from the nature of matter to the emergence of life itself.

The Black Body Problem and Ultraviolet Catastrophe

As the nineteenth century turned, new technologies such as the light bulb drove increased interest in the interaction between materials and radiation. Efficient engineering of light bulbs demanded a deeper understanding of how materials absorb and emit energy, especially the filaments inside the bulbs. In the early 1890s, the German Bureau of Standards commissioned Planck to optimize light bulb efficiency by identifying the temperature at which bulbs would radiate mainly in the visible spectrum while minimizing energy loss in the ultraviolet and infrared regions [1].

Prior attempts to explain the behaviour of heated materials, notably the Raleigh-Jeans law, predicted infinite energy emission at short wavelengths – the so-called ultraviolet catastrophe. These models often relied on the concept of an ideal material that perfectly absorbs all wavelengths, termed a black body. The ultraviolet catastrophe led directly to the “black body problem,” as experimental results contradicted the notion that materials like lightbulb filaments would emit infinite energy at high temperatures.

Planck addressed this issue by conducting experiments with electrically charged oscillators in cavities filled with black body radiation. He discovered that the oscillator could only change its energy in minimal increments, later quantified as h (Planck’s constant). The energy exchanged was proportional to the frequency of the electromagnetic wave and occurred in discrete quantities, or quanta. This finding gave rise to quantum theory and revealed a deeper truth: energy remains with the oscillator (or the atoms in the material) even at absolute zero temperature.

Zero-Point Energy and Its Implications

By solving the ultraviolet catastrophe through his black body absorption equation, Planck discovered zero-point energy (ZPE). Unlike the catastrophe, the existence of zero-point energy was verified experimentally, overturning classical thermodynamics’ expectation that all molecular motion would cease at absolute zero.

Zero-point energy accounts for phenomena such as vacuum-state fluctuations, where even an electromagnetic field with no photons is not truly empty but exhibits constant fluctuations due to ZPE. One of the most fascinating examples is the Gecko – a lizard capable of traversing walls and ceilings on nearly any material. The Gecko exploits quantum vacuum fluctuations present in the zero-point energy of the electromagnetic field. Its feet are covered with millions of microscopic hairs that interact with the quantum vacuum fluctuations of any nearby surface, resulting in an attractive force known as van der Waals force, a microscopic form of the Casimir effect. Through this process, the Gecko draws energy from the vacuum field, demonstrating nature’s ability to harness zero-point energy.

Experimental Advances in Harnessing Zero-Point Energy

Research teams from Purdue University and the University of Colorado Boulder have shown that energy from the vacuum state can be accessed through the Casimir force, which acts on micro-sized plates in experimental setups. Although the effect is small and produces limited energy, more efficient methods may be possible using quantum vacuum density and spin. The impact of spin is visible in fluid systems like hurricanes and tornadoes. By inducing high angular momentum vortices with plasma coupled to the quantum vacuum, researchers can create energy gradients much larger than those observed with simple non-conductive plates in the Casimir effect.

These pioneering investigations illuminate how quantum phenomena, once confined to abstract theory, are now being harnessed in the laboratory to extract measurable effects from the very fabric of space. While the practical application of zero-point energy remains in its infancy, the ongoing refinement of experimental techniques – such as manipulating spin and plasma interactions – offers glimpses of a future where the subtle energy fields underlying all matter could become a resource for technological innovation. Each advance deepens our appreciation for the intricate interplay between quantum mechanics and the observable world, suggesting that the restless energy pervading the vacuum is not merely a curiosity, but a potential wellspring of discovery and transformation that may one day reshape our understanding of both energy and existence.

Conclusion

Max Planck’s pursuit to optimize the humble light bulb did far more than revolutionize technology, it opened a window into the deepest workings of the universe. By questioning how filaments absorb and emit energy, Planck uncovered the quantum nature of reality, revealing that energy is exchanged in discrete packets, or quanta, rather than in a continuous flow. This insight not only solved the black body problem and the ultraviolet catastrophe but also led to the discovery of zero-point energy, the realization that even at absolute zero, particles never truly rest, and the universe itself is in perpetual motion. 

Zero-point energy shows us that nothing in the cosmos is permanent. Particles continuously move, shift, and even appear and disappear, embodying a universe that is dynamic and ever-changing. As humans, we are inseparable from this cosmic dance. Our bodies, thoughts, and lives are woven from the same quantum fabric, always in flux, always evolving. Planck’s work reminds us that change is not just inevitable, it is fundamental to existence itself. In understanding zero-point energy, we come to see that reality is not a static backdrop, but a vibrant, restless sea of possibility, where both matter and meaning are constantly being created and transformed.

by Tags: , , , , , , Leave a comment

Exploring the Implications of Quantum Collapse on Computing

The measurement problem isn’t just theoretical; it directly affects the development of effective quantum computing … Ultimately, reducing errors and increasing algorithm success in quantum computing relies on a solid grasp of what happens during measurement.

Introduction

In quantum mechanics, superposition refers to a unique and intriguing phenomenon where quantum particles can exist in several states simultaneously. Without observation, a quantum system remains in superposition and continues to evolve following Schrödinger’s equation. However, when we measure the system, it collapses into a single, definite state.

This concept challenges our everyday experience with classical objects, which always appear to have specific, identifiable states. Numerous experiments have confirmed that atoms can occupy two or more distinct energy levels at once [1]. If undisturbed, an atom stays in superposition until measurement causes its quantum state to break and settle into one outcome.

But what does it mean to measure or observe a quantum system? Why should a system capable of existing in countless simultaneous states reduce to just one when observed? These fundamental questions form the core of the “measurement problem” in quantum mechanics, a puzzle that has intrigued scientists for over a century since the field was first developed.

The measurement problem

The concept of “measurement,” as addressed by the wave function, has long raised critical questions regarding both the scientific and philosophical underpinnings of quantum mechanics, with significant implications for our comprehension of reality. Numerous interpretations exist to explain the measurement problem, which continues to challenge efforts to establish a coherent and reliable account of the nature of reality. Despite over a century of advancement in quantum mechanics, definitive consensus remains elusive concerning its most fundamental phenomena, including superposition and entanglement.

Quantum mechanics dictates that a quantum state evolves according to two distinct processes: if undisturbed, it follows Schrödinger’s equation; when subjected to measurement, the system yields a classical outcome, with probabilities determined by the Born rule. Measurement refers to any interaction extracting classical information from a quantum system probabilistically, without facilitating communication between remote systems [2]. This framework allows the measurement problem to be categorized into three principal issues:

  • Preferred basis problem – during measurement, outcomes consistently manifest within a particular set of states, although quantum states can, in theory, be described by infinitely many mathematical representations.
  • Non-observability of interference problem – observable interference effects arising from coherent superpositions are limited to microscopic scales.
  • Outcomes problem – measurements invariably produce a single, definitive result rather than a superposition of possibilities. The mechanism behind this selection and its implications for observing superposed outcomes remain unclear.

Addressing any one of these challenges does not fully resolve the others, thereby perpetuating the complexities inherent in the measurement problem.

Wave function collapse

The superposition of an atom across all possible states is characterized by a wave function, which serves as a representation of every quantum state and the probability associated with each state [3]. This function illustrates how an electron within an atomic cloud may occupy various positions with corresponding probabilities, and similarly how a qubit in a quantum computer can be in both states 0 and 1 simultaneously.

In the absence of observation, the system evolves continuously, maintaining the full spectrum of probabilities. Measurement, however, results in a distinct outcome; the act of measurement compels the selection of a single result from myriad possibilities, causing alternative outcomes to cease. As formalized by John von Neumann in 1932, quantum theory reliably predicts the statistical distribution of results over repeated trials, though it remains impossible to forecast the precise outcome of any individual measurement.

The wave function underscores the inherent randomness in the determination of outcomes, akin to nature employing chance. Albert Einstein famously critiqued this perspective, suggesting it implied that “God is playing dice” with the universe. Despite its counterintuitive nature, the wave function is essential for translating the stochasticity of superposition into the observed singular outcome, determined by the probabilities encoded within the wave function.

Conclusion

Wave function collapse plays a key role in quantum mechanics, linking the quantum and classical worlds. This phenomenon lets us measure things like an electron’s position and operate qubits in quantum computers, ensuring accurate results through coherence. Building dependable quantum computers largely depends on managing wave function collapse, aiming to prevent early collapses and errors while encouraging collapses that yield useful data.

The measurement problem isn’t just theoretical; it directly affects the development of effective quantum computing. Quantum algorithms work by sampling from a superposition of computational paths and collapsing them into desired outcomes, especially when designed well. Wave function collapse determines whether qubits are measured as intended or accidentally disrupted by outside influences (decoherence). Ultimately, reducing errors and increasing algorithm success in quantum computing relies on a solid grasp of what happens during measurement.

by Tags: , , , , , , 1 Comment

Quantum Entanglement: ‘Spooky Action at a Distance’

The atoms that comprise all matter – including those composing our bodies – originated from distant stars and galaxies, emphasizing our intrinsic connection to the universe at fundamental scales. It is perhaps an inescapable conclusion that our reality is defined by how we observe and view our universe, and everything within it.

Introduction

In 1935, Albert Einstein, Boris Podolsky, and Nathan Rosen published a paper addressing the conceptual challenges posed by quantum entanglement [1]. These physicists argued that quantum entanglement appeared to conflict with established physical laws, and suggested that existing explanations were incomplete without the inclusion of undiscovered properties, referred to as hidden variables. This argument, later termed the EPR argument, underscored perceived gaps in quantum mechanics.

Quantum entanglement represents a significant and intriguing phenomenon within quantum mechanics. It describes a situation wherein the characteristics of one particle within an entangled pair are dependent on those of its partner, regardless of the spatial separation between them. The particles involved may be electrons or photons, with properties such as spin direction serving as examples. Fundamentally, entanglement is based on quantum superposition: particles occupy multiple potential states until observation forces the system into a definite state. This state collapse occurs instantaneously for both particles.

The implication that measuring one particle’s property immediately determines the corresponding property of the other – even across vast cosmic distances – suggests the transmission of information at speeds exceeding that of light. This notion appeared to contradict foundational principles of physics as understood by Einstein, who referred to quantum entanglement as “spooky action at a distance” and advocated for a more satisfactory theoretical explanation.

Modern understanding of entanglement

The EPR argument highlighted the conventional concept of reality as consisting of entities with physical properties that are revealed through measurement. Einstein’s theory of relativity is based on this perspective, asserting that reality must be local and that no influence can propagate faster than the speed of light [2]. The EPR analysis demonstrated that quantum mechanics does not align with these principles of local reality, suggesting that a more comprehensive theory may be required to fully describe physical phenomena.

It was not until the 1960s that advances in technology and clearer definitions of measurement permitted physicists to investigate whether hidden variables were necessary to complete quantum theory. In 1964, Irish physicist John S. Bell formulated an equation, Bell’s inequality, which holds true for hidden variable theories but not exclusively for quantum mechanics. If real-world experiments failed to satisfy Bell’s equation, hidden variables could be excluded as an explanation for quantum entanglement.

In 2022, the Nobel Prize in Physics honored Alain Aspect, John Clauser, and Anton Zeilinger for their pioneering experiments utilizing Bell’s inequality, which significantly advanced our understanding of quantum entanglement. Unlike earlier thought experiments involving pairs of electrons and positrons, their work employed entangled photons. Their findings definitively eliminated the possibility of hidden variables and confirmed that particles can exhibit correlations across vast distances, challenging pre-quantum mechanical interpretations of physics.

Furthermore, these experiments demonstrated that quantum mechanics is compatible with special relativity. The collapse of the states of two entangled particles upon measurement does not entail information transfer exceeding the speed of light; rather, it reveals a correlation between entangled particle states governed by randomness and probability, such that measuring one immediately determines the state of the other.

Conclusion

When he called it “spooky action at a distance”, Einstein sought to understand entanglement within the context of local reality. The EPR argument subsequently highlighted the non-local nature of reality through quantum entanglement. Although information cannot be transmitted faster than the speed of light, quantum entanglement demonstrates that the states of entangled particles exhibit instantaneous correlations, ensuring that any transfer of information remains consistent with causality and relativity.

Quantum entanglement underscores the indeterminate nature of reality prior to observation. Rather than existing as predetermined outcomes, reality according to quantum systems resides within vast fields of probability that are defined upon measurement. Additionally, the atoms that comprise all matter – including those composing our bodies – originated from distant stars and galaxies, emphasizing our intrinsic connection to the universe at fundamental scales. It is perhaps an inescapable conclusion that our reality is defined by how we observe and view our universe, and everything within it.

by Tags: , , , , , , , , , 2 Comments